pourquoi Python ?¶
conçu pour être lisible, syntaxe simple
pas de délimitations
begin end ; {}uniquement des indentations
la lisibilité fait partir de l’ADN du langage
typage dynamique
pas de perte de temps à l’écriture des programmes
portable
Windows, Linux, Mac OS, etc.
pourquoi Python ? : lisible¶
# le sucre syntaxique est réduit au minimum
# c'est un partis-pris de conception
# le code est lisible par construction
def factorielle(n):
if n <= 1:
return 1
else:
return n * factorielle(n-1)factorielle(0)1factorielle(8)40320trop long ?
bien sûr on peut aussi écrire de façon plus concise si on préfère, comme par ex.
def factorielle(n):
return 1 if n <= 1 else n * factorielle(n-1)pourquoi Python ? : puissant (batteries included)¶
types disponibles très puissants et flexibles
entiers non bornés, nombres complexes
listes, strings Unicode
tables de hash: dictionnaires et ensembles
langage orienté objet: définir ses propres types
énorme base de librairies
et s’interface facilement avec C et C++
et donc du code efficace
gestion de la mémoire automatique
GC
pourquoi Python ? : pas de compilation¶
langage interprété
script direct en ligne de commande
REPL: usage interactif (ipython / notebook)
pré-compilation en byte-code des programmes (.pyc)
totalement transparent
mais pas non plus optimisé comme du code machine..
pourquoi python ? : ouvert et gratuit¶
notamment toutes les discussions sont en ligne et hébergées sur un site discourse ici
https://
notamment, si vous êtes intéressé aux évolutions du langage:
https://
la Python Software Foundation (PSF)¶
possède les droits sur Python et assure son développement
essentiellement aucune restriction sur le code Python et son usage, même commercial
https://
docs .python .org /3 /license .html
adapté à un très vaste spectre d’usages
philosophie python¶
# le zen de Python est capturé dans un module idoine
import thisThe Zen of Python, by Tim Peters
Beautiful is better than ugly.
Explicit is better than implicit.
Simple is better than complex.
Complex is better than complicated.
Flat is better than nested.
Sparse is better than dense.
Readability counts.
Special cases aren't special enough to break the rules.
Although practicality beats purity.
Errors should never pass silently.
Unless explicitly silenced.
In the face of ambiguity, refuse the temptation to guess.
There should be one-- and preferably only one --obvious way to do it.
Although that way may not be obvious at first unless you're Dutch.
Now is better than never.
Although never is often better than *right* now.
If the implementation is hard to explain, it's a bad idea.
If the implementation is easy to explain, it may be a good idea.
Namespaces are one honking great idea -- let's do more of those!
quelle version de python ?¶
version 3.x
conseil: ne pas utiliser un trait spécifique à la toute dernière version pour du code à large diffusion
une version par an (actuellement 3.13)
minimum recommandé (aujourd’hui en 2025): 3.10
ne plus utiliser 2.x !
la version 2.7 est morte et enterré (a été supportée jusque 1er janvier 2020)
de moins en moins problématique (mais attention sur MacOS !)
comment lancer python ?¶
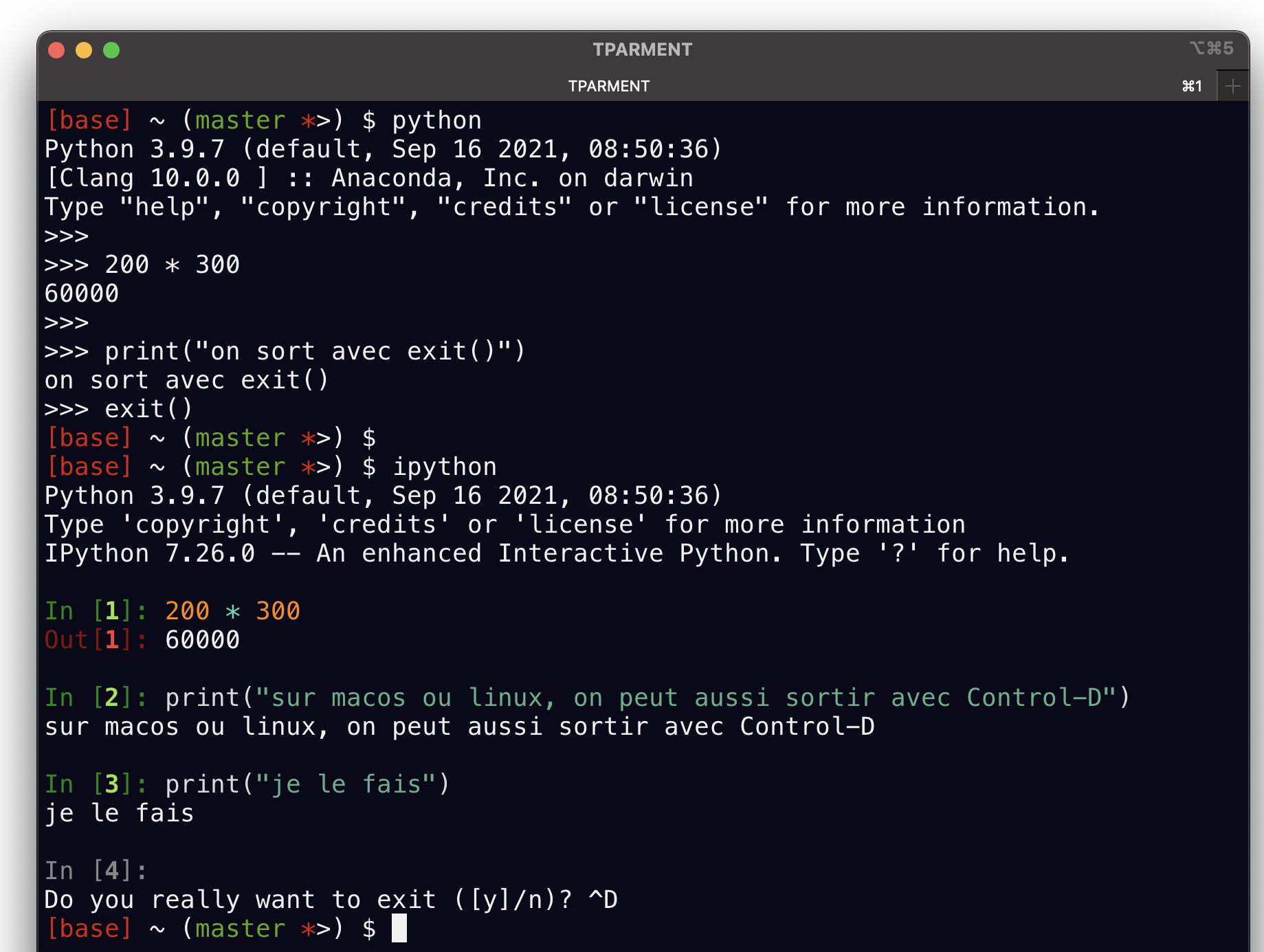
depuis un terminal ...¶
taper
pythondans le terminalinterpréteur en ligne de commande
en option,
ipythonen remplacementnécessite une installation supplémentaire
pip install ipython
dans le terminal toujours:
pip install mylibraryest la façon standard d’installer une librairie externepython -m pip install mylibraryest équivalent, et parfois plus approprié, notamment en cas d’installation biscornue
... ou dans un environnement graphique¶
Jupyter notebooks
# pour installer pip install jupyterlab # et ensuite pour démarrer la session de notebooks jupyter labIDE de votre choix (vs-code, PyCharm, SublimeText,
atom, eclipse, ... bcp de variantes)
dans tous les cas,
faites un premier test:
100 * 10010000il faut savoir interrompre/redémarrer son interpréteur !
par exemple dans jupyter lab voyez le menu Kernel
comment avoir de l’aide¶
dir()¶
dir(objet)retourne les attributs d’un objet
utile notamment sur un module
import math
dir(math)['__doc__',
'__loader__',
'__name__',
'__package__',
'__spec__',
'acos',
'acosh',
'asin',
'asinh',
'atan',
'atan2',
'atanh',
'cbrt',
'ceil',
'comb',
'copysign',
'cos',
'cosh',
'degrees',
'dist',
'e',
'erf',
'erfc',
'exp',
'exp2',
'expm1',
'fabs',
'factorial',
'floor',
'fmod',
'frexp',
'fsum',
'gamma',
'gcd',
'hypot',
'inf',
'isclose',
'isfinite',
'isinf',
'isnan',
'isqrt',
'lcm',
'ldexp',
'lgamma',
'log',
'log10',
'log1p',
'log2',
'modf',
'nan',
'nextafter',
'perm',
'pi',
'pow',
'prod',
'radians',
'remainder',
'sin',
'sinh',
'sqrt',
'sumprod',
'tan',
'tanh',
'tau',
'trunc',
'ulp']help()¶
help(objet)retourne une aide en ligne sur l’objet
utile sur fonctions, méthodes, classes, modules
fonctionne dans tous les environnements
# sur tout un module
help(math)Help on built-in module math:
NAME
math
DESCRIPTION
This module provides access to the mathematical functions
defined by the C standard.
FUNCTIONS
acos(x, /)
Return the arc cosine (measured in radians) of x.
The result is between 0 and pi.
acosh(x, /)
Return the inverse hyperbolic cosine of x.
asin(x, /)
Return the arc sine (measured in radians) of x.
The result is between -pi/2 and pi/2.
asinh(x, /)
Return the inverse hyperbolic sine of x.
atan(x, /)
Return the arc tangent (measured in radians) of x.
The result is between -pi/2 and pi/2.
atan2(y, x, /)
Return the arc tangent (measured in radians) of y/x.
Unlike atan(y/x), the signs of both x and y are considered.
atanh(x, /)
Return the inverse hyperbolic tangent of x.
cbrt(x, /)
Return the cube root of x.
ceil(x, /)
Return the ceiling of x as an Integral.
This is the smallest integer >= x.
comb(n, k, /)
Number of ways to choose k items from n items without repetition and without order.
Evaluates to n! / (k! * (n - k)!) when k <= n and evaluates
to zero when k > n.
Also called the binomial coefficient because it is equivalent
to the coefficient of k-th term in polynomial expansion of the
expression (1 + x)**n.
Raises TypeError if either of the arguments are not integers.
Raises ValueError if either of the arguments are negative.
copysign(x, y, /)
Return a float with the magnitude (absolute value) of x but the sign of y.
On platforms that support signed zeros, copysign(1.0, -0.0)
returns -1.0.
cos(x, /)
Return the cosine of x (measured in radians).
cosh(x, /)
Return the hyperbolic cosine of x.
degrees(x, /)
Convert angle x from radians to degrees.
dist(p, q, /)
Return the Euclidean distance between two points p and q.
The points should be specified as sequences (or iterables) of
coordinates. Both inputs must have the same dimension.
Roughly equivalent to:
sqrt(sum((px - qx) ** 2.0 for px, qx in zip(p, q)))
erf(x, /)
Error function at x.
erfc(x, /)
Complementary error function at x.
exp(x, /)
Return e raised to the power of x.
exp2(x, /)
Return 2 raised to the power of x.
expm1(x, /)
Return exp(x)-1.
This function avoids the loss of precision involved in the direct evaluation of exp(x)-1 for small x.
fabs(x, /)
Return the absolute value of the float x.
factorial(n, /)
Find n!.
Raise a ValueError if x is negative or non-integral.
floor(x, /)
Return the floor of x as an Integral.
This is the largest integer <= x.
fmod(x, y, /)
Return fmod(x, y), according to platform C.
x % y may differ.
frexp(x, /)
Return the mantissa and exponent of x, as pair (m, e).
m is a float and e is an int, such that x = m * 2.**e.
If x is 0, m and e are both 0. Else 0.5 <= abs(m) < 1.0.
fsum(seq, /)
Return an accurate floating point sum of values in the iterable seq.
Assumes IEEE-754 floating point arithmetic.
gamma(x, /)
Gamma function at x.
gcd(*integers)
Greatest Common Divisor.
hypot(...)
hypot(*coordinates) -> value
Multidimensional Euclidean distance from the origin to a point.
Roughly equivalent to:
sqrt(sum(x**2 for x in coordinates))
For a two dimensional point (x, y), gives the hypotenuse
using the Pythagorean theorem: sqrt(x*x + y*y).
For example, the hypotenuse of a 3/4/5 right triangle is:
>>> hypot(3.0, 4.0)
5.0
isclose(a, b, *, rel_tol=1e-09, abs_tol=0.0)
Determine whether two floating point numbers are close in value.
rel_tol
maximum difference for being considered "close", relative to the
magnitude of the input values
abs_tol
maximum difference for being considered "close", regardless of the
magnitude of the input values
Return True if a is close in value to b, and False otherwise.
For the values to be considered close, the difference between them
must be smaller than at least one of the tolerances.
-inf, inf and NaN behave similarly to the IEEE 754 Standard. That
is, NaN is not close to anything, even itself. inf and -inf are
only close to themselves.
isfinite(x, /)
Return True if x is neither an infinity nor a NaN, and False otherwise.
isinf(x, /)
Return True if x is a positive or negative infinity, and False otherwise.
isnan(x, /)
Return True if x is a NaN (not a number), and False otherwise.
isqrt(n, /)
Return the integer part of the square root of the input.
lcm(*integers)
Least Common Multiple.
ldexp(x, i, /)
Return x * (2**i).
This is essentially the inverse of frexp().
lgamma(x, /)
Natural logarithm of absolute value of Gamma function at x.
log(...)
log(x, [base=math.e])
Return the logarithm of x to the given base.
If the base is not specified, returns the natural logarithm (base e) of x.
log10(x, /)
Return the base 10 logarithm of x.
log1p(x, /)
Return the natural logarithm of 1+x (base e).
The result is computed in a way which is accurate for x near zero.
log2(x, /)
Return the base 2 logarithm of x.
modf(x, /)
Return the fractional and integer parts of x.
Both results carry the sign of x and are floats.
nextafter(x, y, /, *, steps=None)
Return the floating-point value the given number of steps after x towards y.
If steps is not specified or is None, it defaults to 1.
Raises a TypeError, if x or y is not a double, or if steps is not an integer.
Raises ValueError if steps is negative.
perm(n, k=None, /)
Number of ways to choose k items from n items without repetition and with order.
Evaluates to n! / (n - k)! when k <= n and evaluates
to zero when k > n.
If k is not specified or is None, then k defaults to n
and the function returns n!.
Raises TypeError if either of the arguments are not integers.
Raises ValueError if either of the arguments are negative.
pow(x, y, /)
Return x**y (x to the power of y).
prod(iterable, /, *, start=1)
Calculate the product of all the elements in the input iterable.
The default start value for the product is 1.
When the iterable is empty, return the start value. This function is
intended specifically for use with numeric values and may reject
non-numeric types.
radians(x, /)
Convert angle x from degrees to radians.
remainder(x, y, /)
Difference between x and the closest integer multiple of y.
Return x - n*y where n*y is the closest integer multiple of y.
In the case where x is exactly halfway between two multiples of
y, the nearest even value of n is used. The result is always exact.
sin(x, /)
Return the sine of x (measured in radians).
sinh(x, /)
Return the hyperbolic sine of x.
sqrt(x, /)
Return the square root of x.
sumprod(p, q, /)
Return the sum of products of values from two iterables p and q.
Roughly equivalent to:
sum(itertools.starmap(operator.mul, zip(p, q, strict=True)))
For float and mixed int/float inputs, the intermediate products
and sums are computed with extended precision.
tan(x, /)
Return the tangent of x (measured in radians).
tanh(x, /)
Return the hyperbolic tangent of x.
trunc(x, /)
Truncates the Real x to the nearest Integral toward 0.
Uses the __trunc__ magic method.
ulp(x, /)
Return the value of the least significant bit of the float x.
DATA
e = 2.718281828459045
inf = inf
nan = nan
pi = 3.141592653589793
tau = 6.283185307179586
FILE
(built-in)
# ou juste une fonction
help(math.factorial)Help on built-in function factorial in module math:
factorial(n, /)
Find n!.
Raise a ValueError if x is negative or non-integral.
complétion¶
apprenez à utiliser <TAB> pour la complétion!!
cela fait ggner un temps fou !
et d’ailleurs pas que dans jupyter, c’est pervasif: dans le shell/terminal, dans vs-code, etc...
# tapez le début
# math.fac
# puis à ce stade taper <TAB>
# ce qui va vous aider à finir la phrase avec un mot connusi votre début de phrase est trop flou, vous aurez à choisir dans une liste de possibles
dans ce cas, utilisez le clavier pour sélectionner la bonne
# tapez ceci
# math.
# et là si vous tapez <TAB> on va vous afficher les possibilités
# c'est à dire en gros le contenu de dir(math) comme on l'a vu plus haut
# mais c'est interactifaide avec symbol?¶
pour obtenir de l’aide dans une fenêtre dédiée avec
?le symbole doit être connu de python
comme pour les % qu’on a vus un peu plus haut, cette notation avec le ? ne fonctionne pas dans le python “de base”
il faut être soit dans IPython, soit dans un notebook
math?math.factorial?aide avec symbol??¶
avec un double ?? on peut avoir accès au code source
# bien sûr il faut avoir **évalué** l'import
from argparse import ArgumentParser# avant de pouvoir instrospecter l'objet ArgumentParser
ArgumentParser??documentation¶
personnellement, pour un accès rapide à la documentation, je fais très facilement une recherche google genre
python module datetime
que l’on peut consulter aussi comme ceci
https://
fourni avec Python¶
site officiel de la doc Python
aussi en français ici https://
docs .python .org /fr /3/ très riche: du tutoriel à la description du langage
contient notamment le Python tutorial
initialement Guido van Rossum
niveau débutant à moyen
des cours¶
MOOC Python : des fondamentaux à l’utilisation du langage
A. Legout et T. Parmentelat
MOOC : apprendre à coder en Python un peu plus simple
http://
fr .openclassrooms .com /informatique /cours /apprenez -a -programmer -en -python et sans doute des dizaines d’autres
et aussi¶
l’incontournable stackoverflow (SO)
https://
stackoverflow .com /questions /tagged /python+python -3.x on peut directement chercher sur Google
enfin pour ceux qui aiment les cheat sheet
quand utiliser python ?¶
scripts (mais pas uniquement ça!)
programmation système
Internet
base de données
prototypage rapide
calcul scientifique avec
numpyexploration dans les données avec
pandasetscikit-learnbackend web avec
Django/Flask…
quand ne pas utiliser Python ?¶
Python est plutôt gourmand en mémoire
tout est objet ➔ surcoût partout
exemples sur une machine 64 bits
| objet | octets | natif C |
|---|---|---|
| petit entier | 28 octets | 8 octets |
| chaine ‘a’ | 50 octets | 1 octet |
| chaine ‘é’ | 74 octets | 2 octets |
Python plutôt bon en termes de vitesse
fonctions de base implémentées en C optimisé
PyPy très rapide par rapport à CPython
pensez à utiliser
numpy
comment prendre la décision d’utiliser Python ?¶
balancer vitesse de développement avec performance
Python gagne presque toujours
comment tester la performance ?¶
%%timeit
# on construit la liste des premiers carrés
[x**2 for x in range(10000)]The slowest run took 6.37 times longer than the fastest. This could mean that an intermediate result is being cached.
1.04 ms ± 827 μs per loop (mean ± std. dev. of 7 runs, 1,000 loops each)
cette construction avec les % n’est pas standard Python, c’est une magic de IPython
on ne peut l’utiliser que dans ipython ou dans les notebooks
comment tester la place mémoire ?¶
# retourne le nombre d'octets
# utilisés pour stoker un objet
import sys
sys.getsizeof([10])64sys.getsizeof([10, 20])72sys.getsizeof([10, 20, 30])88